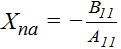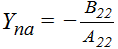The elastic properties (i.e. stiffnesses) are calculated for the effective laminate from classical lamination theory. Whether the effective laminate is calculated using the manual method or the automated method, the calculation of effective properties are the same. With the automated method, you will not see the ABD matrix calculations, but if you use the Laminate Analysis form, you can trace the terms that HyperSizer is calculating.

These are the stiffness terms form classical lamination theory which relate laminate force and moment to strain and curvature. Only isotropic and orthotropic plies are included. All other materials (foam, honeycomb, etc.) are treated as empty space where the proper offsets are maintained, however, the stiffnesses of these materials will not contribute to the ABD terms. For details on classical lamination theory, see the references below [Jones, 1999].
These terms are an extension of the classical lamination theory ABD matrix for relating thermal strain (εα) and curvature (κα) with temperature changes (ΔT) and through-thickness temperature gradients (ΔG). The derivations of these terms can be found in the references [Collier, 1993].

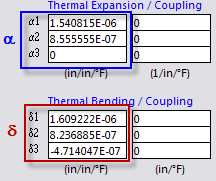
The thermal term α (a 3x1 vector) represents the relationship between strain and temperature change, and δ (a 3x1 vector) represents the relationship between curvature and the through-thickness temperature gradient. The coupling terms, αc and δc relate strain to the through-thickness gradient and curvature to the temperature change, respectively. The coupling terms will always be zero for a symmetric laminate.
These are laminate stiffness properties that approximate the laminate as an isotropic material. The notation (A11)-1 denotes the 11 value of the inverted A matrix.
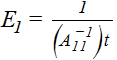
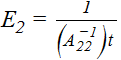
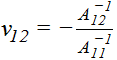
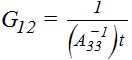
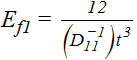
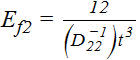
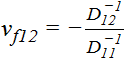

The thermal expansion terms in the effective laminate are the same α1 and α2 thermal terms shown on the Laminate Analysis form under Thermal Expansion / Bending / Coupling. The thermal bending and coupling terms (δ, αc, δc)are not included in the effective laminate.
Two neutral axes are defined. The x-neutral axis is the fiber location relative to the reference plane at which an applied Nx load induces zero x-curvature. The y-neutral axis relates Ny load to y-curvature in the same way.