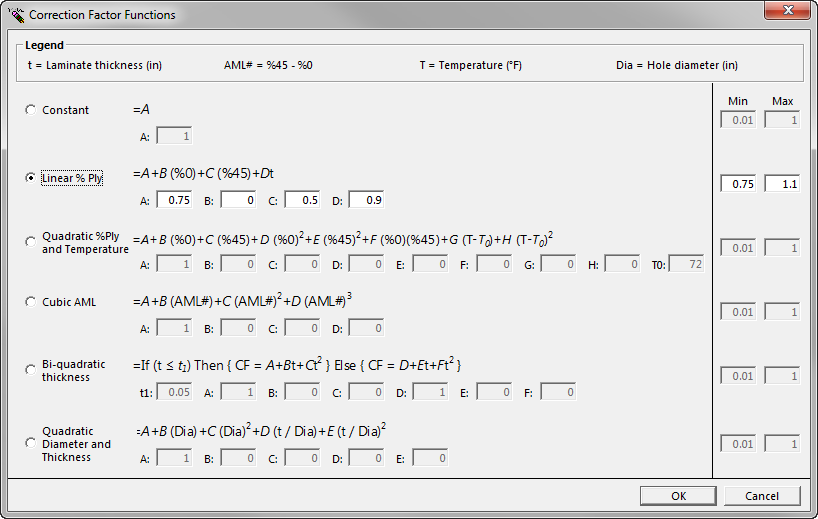
Features > Materials > Orthotropic Correction Factors > Correction Factor Functions

Correction Factor Functions

There are six correction factor methods, as shown above, that can be used to define the lamina corrections including linear and quadratic functions of laminate geometry, temperature, and hole diameter. The polynomial equations can theoretically be as generic as you wish. In this example, the linear percent ply approach is selected to knockdown the e_OHC ply allowable with the following function:

e_OHC=0.75+0.5(%45)+0.9(t)

Where %45 is the percentage of 45 degree fibers and t is the total laminate thickness.

Min and Max are available to define the upper and lower bounds of the applied correction factors. In the example, the applied correction factor must be between 0.75 and 1.1.

To change any of the correction factor equations, select the desired method and enter the appropriate coefficients. The coefficients A-H are entered as real numbers. Entering a coefficient of 0 will remove that term from the equation.

Constant The correction factor is defined to correct the property value entered on the form. The value must be a non-zero real number. For example, a factor of 1.0 will disable this correction factor.
Linear % Ply The correction factors are defined as a linear function of ply angle percentages (0's and 45's) and laminate thickness.
Quadratic % Ply and Temperature The correction factors are defined as a quadratic function of ply angle percentages (0's and 45's), laminate thickness, and change in temperature. The initial temperature is defined in the T0 box.
Cubic AML The correction factors are defined as a cubic function of the Angle Minus Longitudinal (AML) parameter. The AML parameter characterizes laminate geometry as a function of %0 and %45s:

AML = %±45 - %0

The AML parameter can range between -100 < AML < 100.
Bi-quadratic thickness The correction factors are defined as a piecewise quadratic function of laminate thickness.

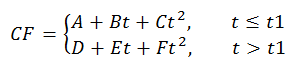
To enter a single quadratic function based on laminate thickness, define coefficients A-C and make the t1 term very high, t1 >> 1.0 inch.
Quadratic Diameter and Thickness The correction factors are defined as a quadratic function of open hole diameter and laminate thickness. The hole diameter (Dia) is defined for a panel or beam object on the Bolted Joint Analysis form.

See Bolted Joint Analysis Form.