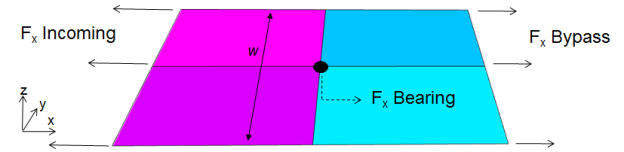
Failure Analysis > Joints > Bolted > Bypass Loads

Bypass Loads

Bypass loads are computed for two of the BJSFM analysis methods:

Joint, Bolted, Single Hole, BJSFM bearing and bypass load
Joint, Bolted, Single Hole, BJSFM bypass load only

These two BJSFM analysis methods include the contribution of the bypass loads. This far field loading causes the hole to elongate, even without bolt bearing. If far field loading is present, it can have a significant impact on reducing the allowable bearing stress.

Force Balance

The bypass load is computed using a force balance that considers the net result of applying bearing force and far field loading.

Σ F_x: F_x,incoming = F_x,bypass + F_x,bearing

(N_x,incoming)w = (N_x,bypass)w + F_x,bearing

The incoming N_x load is not known since FEA loads are processed using element area-based averages. The average N_x load can be expressed as:

N_x,avg = (N_x,incoming + N_x,bypass) / 2

Using the expression above the bypass load can be computed in terms of average N_x.

N_x,bypass = N_x,avg - F_x,bearing/(2w)

This force balance is expanded to include the load angle to compute the bypass load in each primary direction.

N_x,bypass = sign(N_x,avg) * { |N_x,avg | - (P*cos α) / (2*W_Yspan)}

N_y,bypass = sign(N_y,avg) * { |N_y,avg | - (P*sin α) / (2*W_Xspan)}

Where P= bearing force (lb) and α = load angle (0 deg ≤ α ≤ 180 deg).

Note that when tension and compression element loads are present in the component, the true N_x,avg and N_y,avg loads are used to compute the bypass loads.

Finite Width (W)

The finite widths (W) are defined with the component buckling spans.

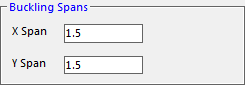
W_Yspan is defined by the Y buckling span.

W_Xspan is defined by the X buckling span.

The finite widths define the area in the laminate that is affected by the presence of the hole. Typically, a multiple of the fastener diameter is used, 3*D.