When a finite element model is imported, the buckling span lengths based on the geometry of the shell elements are automatically calculated. The buckling spans are displayed in the FEM Viewer and on the Buckling tab.
Important: Buckling spans are not recomputed during FEM reimport. This is to prevent user-modified buckling spans from being overwritten.
Buckling spans can be recomputed manually in the FEM Viewer using the Auto Calculate Buckling Span feature.
The sections below describe the algorithm HyperSizer uses to calculate the buckling spans and radius of curvature.
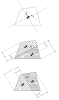
First, the centroid and the equivalent longitudinal and transverse directions for the component are determined from the geometry and material axis orientations of the contained finite elements. Next, the component is divided into two halves along the centroid in the longitudinal direction, two halves in the transverse direction, and the centroid is determined for each half. Finally, the buckling spans in the two directions are determined from the following equations.
Yspan = 2 [min(cy+, (Y+ - cy+)) + min(cy-,(Y--cy-))]
Xspan = 2 [min(cx+, (X+ - cx+)) + min(cx-,(X--cx-))]
Where Y+ and Y- are the distances from the centroid to the extent of the component in the transverse direction, cy+ and cy- are the distances from the centroid of the component to the centroids of the two halves, etc. These distances are defined in the figure below.
For a rectangular component where the longitudinal direction is aligned with the length of the rectangle, the above equations give a longitudinal span equal to the length of the rectangle, and a transverse buckling span length equal to the width of the rectangle. If a component has a triangular shape where the longitudinal direction is aligned with the triangle height, the calculated span will be just over two-thirds the height of the triangle.
As an analyst, it is advisable to review the calculated buckling lengths for each imported component (on the Buckling tab of the Sizing form or using the FEM Viewer) and adjust them as necessary to ensure proper buckling analysis.
Another important component-based property required for buckling analysis is the component Y (transverse) radius of curvature.
In the figure shown below, if a panel is curved in the Y direction, then the curvature, κ, of the panel is found from the equation:
κ = 8D / (4D2 + C2)
Where C is the chord of the cylindrical section and D is the height of the cylindrical section (this formula assumes the cylindrical section is circular). The radius of curvature, R, is then calculated as the inverse of the curvature, 1/κ.
HyperSizer imposes a limit of 50 times the chord length on the radius of curvature. That is, if the calculated radius of curvature is greater than 50C, then the panel is regarded as flat. In the case of a flat panel, the curvature goes to zero and the radius of curvature is infinite. HyperSizer will report a flat panel as having a radius of curvature of zero, which acts as a flag to indicate no curvature.
Important: If the radius of curvature is greater than 50 times the chord length, the panel is imported as flat.
The automated curvature calculation can also handle panels that curve greater than 180° as shown in the figure below. In this case, the chord length is the cylinder diameter and the height is the greater of the upper or lower extents of the cylinder.
As with the buckling span calculation, it is recommended that you review the radius of curvature for each imported component to ensure the proper buckling analysis.
In the previous section, the buckling span length calculation was discussed. However, that calculation assumes that the component is flat. If a panel is curved in the Y-direction, then HyperSizer will adjust the Y Span buckling length to account for the curvature according to the following formula.
Yspan,curved = Yspan,flat [ 2 cos-1(1- κD) / (κD) ]
In addition, the transverse buckling length is limited to quarter the distance around a cylindrical body.
Yspan,curved ≤ π/(2κ)
